Proyekto ng algebra "Paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko" Nakumpleto ng mag-aaral ng klase 10 "B" Kazachkova Yulia Supervisor: guro ng matematika na si Kochakova N.N.
Layunin Upang pagsamahin ang materyal sa paksang "Paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko" at lumikha ng isang paalala para sa mga mag-aaral na maghanda para sa paparating na pagsusulit.
Layunin: Ibuod ang materyal sa paksang ito. I-systematize ang impormasyong natanggap. Pag-isipan ang paksang ito sa Unified State Exam.
Kaugnayan Ang kaugnayan ng paksang pinili ko ay nakasalalay sa katotohanan na ang mga gawain sa paksang "Paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko" ay kasama sa mga gawain ng Pinag-isang Pagsusulit ng Estado.
Trigonometric inequalities Ang hindi pagkakapantay-pantay ay isang ugnayang nag-uugnay sa dalawang numero o expression sa pamamagitan ng isa sa mga palatandaan: (mas malaki kaysa); ≥ (mas malaki sa o katumbas ng). Ang hindi pagkakapantay-pantay ng trigonometric ay isang hindi pagkakapantay-pantay na kinasasangkutan ng mga function ng trigonometriko.
Mga hindi pagkakapantay-pantay ng trigonometriko Ang solusyon ng mga hindi pagkakapantay-pantay na naglalaman ng mga function ng trigonometriko ay binabawasan, bilang panuntunan, sa solusyon ng pinakasimpleng hindi pagkakapantay-pantay ng anyo: sin x>a, sin x a, dahil x a, tg x a,ctg x
Algorithm para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko Sa axis na tumutugma sa isang naibigay na trigonometric function, markahan ang ibinigay na numerical value ng function na ito. Gumuhit ng isang linya sa pamamagitan ng minarkahang punto na nagsasalubong sa bilog ng yunit. Piliin ang mga intersection point ng isang linya at isang bilog, na isinasaalang-alang ang mahigpit o hindi mahigpit na tanda ng hindi pagkakapantay-pantay. Piliin ang arko ng bilog kung saan matatagpuan ang mga solusyon sa hindi pagkakapantay-pantay. Tukuyin ang mga halaga ng anggulo sa simula at pagtatapos ng mga punto ng pabilog na arko. Isulat ang solusyon sa hindi pagkakapantay-pantay na isinasaalang-alang ang periodicity ng ibinigay na trigonometric function.
Mga formula para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosxa; x (arctg a + πn ; + πn). tgx a; x (πn ; arctan + πn). ctgx
Graphic na solusyon pangunahing trigonometriko inequalities sinx >a
Graphical na solusyon ng mga pangunahing trigonometriko na hindi pagkakapantay-pantay sinx Graphical na solusyon ng mga pangunahing trigonometrikong hindi pagkakapantay-pantay cosx >a Graphical na solusyon ng mga pangunahing trigonometriko na hindi pagkakapantay-pantay cosx Graphical na solusyon ng mga pangunahing trigonometrikong hindi pagkakapantay-pantay tgx >a Graphical na solusyon ng mga pangunahing trigonometriko na hindi pagkakapantay-pantay tgx Graphic na solusyon ng mga pangunahing trigonometrikong hindi pagkakapantay-pantay ctgx >a
solusyon sa hindi pagkakapantay-pantay nasa mode online solusyon halos anumang naibigay na hindi pagkakapantay-pantay online. Matematika hindi pagkakapantay-pantay sa online upang malutas ang matematika. Maghanap ng mabilis solusyon sa hindi pagkakapantay-pantay nasa mode online. Ang website na www.site ay nagpapahintulot sa iyo na mahanap solusyon halos anumang ibinigay algebraic, trigonometriko o transendental na hindi pagkakapantay-pantay online. Kapag nag-aaral ng halos anumang sangay ng matematika sa iba't ibang yugto kailangang magdesisyon hindi pagkakapantay-pantay sa online. Upang makakuha kaagad ng sagot, at higit sa lahat tumpak na sagot, kailangan mo ng mapagkukunan na nagbibigay-daan sa iyong gawin ito. Salamat sa site na www.site lutasin ang hindi pagkakapantay-pantay sa online aabutin ng ilang minuto. Ang pangunahing bentahe ng www.site kapag nilulutas ang matematika hindi pagkakapantay-pantay sa online- ito ang bilis at katumpakan ng ibinigay na tugon. Ang site ay kayang lutasin ang anuman algebraic inequalities online, mga hindi pagkakapantay-pantay ng trigonometriko online, transendental na hindi pagkakapantay-pantay online, at hindi pagkakapantay-pantay na may hindi kilalang mga parameter sa mode online. Mga hindi pagkakapantay-pantay nagsisilbing isang makapangyarihang kasangkapang pangmatematika mga solusyon praktikal na mga problema. Sa tulong hindi pagkakapantay-pantay sa matematika posible na magpahayag ng mga katotohanan at relasyon na maaaring mukhang nakakalito at kumplikado sa unang tingin. Hindi kilalang dami hindi pagkakapantay-pantay ay matatagpuan sa pamamagitan ng pagbabalangkas ng problema sa mathematical wika sa anyo hindi pagkakapantay-pantay At magpasya nakatanggap ng gawain sa mode online sa website na www.site. Anuman algebraic inequality, hindi pagkakapantay-pantay ng trigonometriko o hindi pagkakapantay-pantay naglalaman ng transendental mga tampok na maaari mong madaling magpasya online at makuha ang eksaktong sagot. Nag-aaral natural na Agham, hindi maiiwasang harapin mo ang pangangailangan mga solusyon sa hindi pagkakapantay-pantay. Sa kasong ito, ang sagot ay dapat na tumpak at dapat makuha kaagad sa mode online. Samakatuwid para sa lutasin ang mga hindi pagkakapantay-pantay sa matematika online inirerekumenda namin ang site na www.site, na magiging iyong kailangang-kailangan na calculator para sa paglutas ng mga algebraic inequalities online, mga hindi pagkakapantay-pantay ng trigonometriko online, at transendental na hindi pagkakapantay-pantay online o hindi pagkakapantay-pantay na may hindi kilalang mga parameter. Para sa mga praktikal na problema sa paghahanap ng mga online na solusyon sa iba't ibang hindi pagkakapantay-pantay sa matematika mapagkukunan www.. Paglutas hindi pagkakapantay-pantay sa online sa iyong sarili, ito ay kapaki-pakinabang upang suriin ang natanggap na sagot gamit online na solusyon hindi pagkakapantay-pantay sa website na www.site. Kailangan mong isulat nang tama ang hindi pagkakapantay-pantay at agad na makuha online na solusyon, pagkatapos ang natitira na lang ay ihambing ang sagot sa iyong solusyon sa hindi pagkakapantay-pantay. Ang pagsuri sa sagot ay tatagal ng hindi hihigit sa isang minuto, sapat na lutasin ang hindi pagkakapantay-pantay sa online at ihambing ang mga sagot. Makakatulong ito sa iyo na maiwasan ang mga pagkakamali sa desisyon at itama ang sagot sa oras paglutas ng mga hindi pagkakapantay-pantay sa online alinman algebraic, trigonometriko, transendental o hindi pagkakapantay-pantay na may hindi kilalang mga parameter.
MGA PARAAN PARA SA PAGLUTAS NG MGA TRIGONOMETRI INEQUALITIES
Kaugnayan. Sa kasaysayan, ang mga trigonometric equation at hindi pagkakapantay-pantay ay binigyan ng espesyal na lugar sa kurikulum ng paaralan. Masasabing ang trigonometrya ay isa sa ang pinakamahalagang seksyon kurso sa paaralan at lahat ng agham sa matematika sa pangkalahatan.
Ang mga equation at hindi pagkakapantay-pantay ng trigonometric ay sumasakop sa isa sa mga pangunahing lugar sa kursong matematika ng sekondaryang paaralan, kapwa sa mga tuntunin ng nilalaman ng materyal na pang-edukasyon at mga pamamaraan ng aktibidad na pang-edukasyon at nagbibigay-malay na maaari at dapat mabuo sa panahon ng kanilang pag-aaral at ilapat sa solusyon. Malaking numero mga problema ng teoretikal at inilapat na kalikasan.
Solusyon trigonometriko equation at ang mga hindi pagkakapantay-pantay ay lumilikha ng mga kinakailangan para sa pagsasaayos ng kaalaman ng mga mag-aaral na may kaugnayan sa lahat materyal na pang-edukasyon sa trigonometrya (halimbawa, mga katangian ng mga function ng trigonometriko, mga paraan ng pagbabago ng mga trigonometriko na expression, atbp.) at ginagawang posible na magtatag ng mga epektibong koneksyon sa pinag-aralan na materyal sa algebra (mga equation, equivalence ng mga equation, hindi pagkakapantay-pantay, magkaparehong pagbabago ng mga algebraic expression, atbp. .).
Sa madaling salita, ang pagsasaalang-alang ng mga pamamaraan para sa paglutas ng mga trigonometric equation at hindi pagkakapantay-pantay ay nagsasangkot ng isang uri ng paglipat ng mga kasanayang ito sa bagong nilalaman.
Ang kahalagahan ng teorya at ang maraming aplikasyon nito ay patunay ng kaugnayan ng napiling paksa. Ito naman ay nagpapahintulot sa iyo na matukoy ang mga layunin, layunin at paksa ng pananaliksik ng gawaing kurso.
Layunin ng pag-aaral: gawing pangkalahatan ang magagamit na mga uri ng hindi pagkakapantay-pantay ng trigonometriko, mga pangunahing at espesyal na pamamaraan para sa paglutas ng mga ito, pumili ng isang hanay ng mga problema para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko ng mga mag-aaral.
Layunin ng pananaliksik:
1. Batay sa pagsusuri ng mga magagamit na literatura sa paksa ng pananaliksik, sistematiko ang materyal.
2. Magbigay ng isang hanay ng mga gawain na kinakailangan upang pagsama-samahin ang paksang "Mga hindi pagkakapantay-pantay ng trigonometriko."
Layunin ng pag-aaral ay mga hindi pagkakapantay-pantay ng trigonometriko sa kursong matematika ng paaralan.
Paksa ng pag-aaral: mga uri ng hindi pagkakapantay-pantay ng trigonometriko at mga pamamaraan para sa paglutas ng mga ito.
Teoretikal na kahalagahan ay ang pag-systematize ng materyal.
Praktikal na kahalagahan: aplikasyon ng teoretikal na kaalaman sa paglutas ng mga problema; pagsusuri ng mga pangunahing karaniwang pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko.
Mga pamamaraan ng pananaliksik : pagsusuri siyentipikong panitikan, synthesis at generalization ng nakuhang kaalaman, pagsusuri ng paglutas ng problema, paghahanap ng pinakamainam na pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay.
§1. Mga uri ng hindi pagkakapantay-pantay ng trigonometriko at mga pangunahing pamamaraan para sa paglutas ng mga ito
1.1. Ang pinakasimpleng hindi pagkakapantay-pantay ng trigonometriko
Dalawang trigonometric expression na konektado ng sign o > ay tinatawag na trigonometric inequalities.
Ang paglutas ng hindi pagkakapantay-pantay ng trigonometric ay nangangahulugan ng paghahanap ng hanay ng mga halaga ng mga hindi alam na kasama sa hindi pagkakapantay-pantay kung saan nasiyahan ang hindi pagkakapantay-pantay.
Ang pangunahing bahagi ng mga hindi pagkakapantay-pantay ng trigonometriko ay nalulutas sa pamamagitan ng pagbabawas ng mga ito sa pinakasimpleng solusyon:
Ito ay maaaring isang paraan ng factorization, pagbabago ng variable ( 
, 
atbp.), kung saan ang karaniwang hindi pagkakapantay-pantay ay unang nalutas, at pagkatapos ay isang hindi pagkakapantay-pantay ng anyo 
atbp., o iba pang mga pamamaraan.
Ang pinakasimpleng hindi pagkakapantay-pantay ay malulutas sa dalawang paraan: gamit ang unit circle o graphical.
Hayaanf(x
– isa sa mga pangunahing function ng trigonometriko. Upang malutas ang hindi pagkakapantay-pantay 
ito ay sapat na upang mahanap ang solusyon nito sa isang panahon, i.e. sa anumang segment na ang haba ay katumbas ng panahon ng functionf
x
. Pagkatapos ang solusyon sa orihinal na hindi pagkakapantay-pantay ay makikita lahatx
, pati na rin ang mga halagang iyon na naiiba sa mga nahanap ng anumang integer na bilang ng mga yugto ng function. Sa kasong ito, maginhawang gamitin ang graphical na paraan.
Magbigay tayo ng isang halimbawa ng isang algorithm para sa paglutas ng mga hindi pagkakapantay-pantay 
(
) At 
.
Algorithm para sa paglutas ng hindi pagkakapantay-pantay (
).
1. Bumuo ng kahulugan ng sine ng isang numerox sa bilog ng yunit.
3. Sa ordinate axis, markahan ang punto ng coordinatea .
4. Gumuhit ng isang linya parallel sa OX axis sa pamamagitan ng puntong ito at markahan ang mga intersection point nito sa bilog.
5. Pumili ng isang arko ng isang bilog, lahat ng mga punto ay may ordinate na mas mababa saa .
6. Ipahiwatig ang direksyon ng pag-ikot (counterclockwise) at isulat ang sagot sa pamamagitan ng pagdaragdag ng panahon ng function sa mga dulo ng pagitan2πn
,
.
Algorithm para sa paglutas ng hindi pagkakapantay-pantay .
1. Bumuo ng kahulugan ng tangent ng isang numerox sa bilog ng yunit.
2. Gumuhit ng bilog na yunit.
3. Gumuhit ng linya ng mga tangent at markahan ang isang punto na may ordinate ditoa .
4. Ikonekta ang puntong ito sa pinanggalingan at markahan ang punto ng intersection ng resultang segment sa bilog ng yunit.
5. Pumili ng isang arko ng isang bilog, ang lahat ng mga punto ay may ordinate sa tangent na linya na mas mababa saa .
6. Ipahiwatig ang direksyon ng traversal at isulat ang sagot na isinasaalang-alang ang domain ng kahulugan ng function, pagdaragdag ng isang tuldokπn
,
(Ang numero sa kaliwa ng entry ay palaging mas mababa kaysa sa numero sa kanan).
Graphic na interpretasyon ng mga solusyon sa mga simpleng equation at formula para sa paglutas ng mga hindi pagkakapantay-pantay sa pangkalahatang pananaw ay ipinahiwatig sa apendiks (Mga Apendise 1 at 2).
Halimbawa 1.
Lutasin ang hindi pagkakapantay-pantay 
.
Gumuhit ng isang tuwid na linya sa bilog ng yunit 
, na nag-intersect sa bilog sa mga puntong A at B.
Lahat ng kahulugany
sa pagitan ng NM ay mas malaki
, lahat ng punto ng AMB arc ay nakakatugon sa hindi pagkakapantay-pantay na ito. Sa lahat ng anggulo ng pag-ikot, malaki 
, ngunit mas maliit 
,
ay magkakaroon ng mga halaga na mas malaki
(ngunit hindi hihigit sa isa).
Fig.1
Kaya, ang solusyon sa hindi pagkakapantay-pantay ay ang lahat ng mga halaga sa pagitan 
, ibig sabihin. 
. Upang makuha ang lahat ng mga solusyon sa hindi pagkakapantay-pantay na ito, sapat na upang idagdag sa mga dulo ng agwat na ito 
, Saan 
, ibig sabihin. 
,
.
Tandaan na ang mga halaga 
At 
ay ang mga ugat ng equation 
,
mga. 
;
.
Sagot: 
, .
1.2. Paraan ng graphic
Sa pagsasagawa, ang graphical na paraan para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko ay kadalasang nagiging kapaki-pakinabang. Isaalang-alang natin ang kakanyahan ng pamamaraan gamit ang halimbawa ng hindi pagkakapantay-pantay 
:
1. Kung kumplikado ang argumento (iba saX ), pagkatapos ay palitan ito ngt .
2. Bumubuo kami sa isang coordinate planetoOy
mga function graph 
At 
.
3. Nakikita natin ang ganyandalawang magkatabing punto ng intersection ng mga graph, sa pagitan ng kung saansine wavematatagpuanmas mataas
tuwid . Natagpuan namin ang abscissas ng mga puntong ito.
4. Sumulat ng dobleng hindi pagkakapantay-pantay para sa argumentot , isinasaalang-alang ang panahon ng cosine (t ay nasa pagitan ng mga natagpuang abscissas).
5. Gumawa ng reverse substitution (bumalik sa orihinal na argumento) at ipahayag ang halagaX mula sa dobleng hindi pagkakapantay-pantay, isinusulat namin ang sagot sa anyo ng isang numerical interval.
Halimbawa 2. Lutasin ang hindi pagkakapantay-pantay: .
Kapag nilulutas ang mga hindi pagkakapantay-pantay gamit ang graphical na pamamaraan, kinakailangan na bumuo ng mga graph ng mga function nang tumpak hangga't maaari. Ibahin natin ang hindi pagkakapantay-pantay sa anyo:
Bumuo tayo ng mga graph ng mga function sa isang coordinate system 
At 
(Larawan 2).
Fig.2
Ang mga graph ng mga function ay nagsalubong sa puntoA
may mga coordinate 
; 
. Sa gitna 
mga punto ng graph 
sa ibaba ng mga graph point 
. At kailan ang mga halaga ng function ay pareho. kaya lang sa 
.
Sagot: 
.
1.3. Algebraic na pamamaraan
Kadalasan, ang orihinal na hindi pagkakapantay-pantay ng trigonometriko ay maaaring gawing algebraic (rasyonal o hindi makatwiran) na hindi pagkakapantay-pantay sa pamamagitan ng isang mahusay na napiling pagpapalit. Ang pamamaraang ito nagsasangkot ng pagbabago ng isang hindi pagkakapantay-pantay, pagpapakilala ng isang pagpapalit, o pagpapalit ng isang variable.
Tingnan natin ang mga partikular na halimbawa ng aplikasyon ng pamamaraang ito.
Halimbawa 3.
Pagbawas sa pinakasimpleng anyo 
.
(Larawan 3)
Fig.3
, 
.
Sagot: 
,
Halimbawa 4. Lutasin ang hindi pagkakapantay-pantay:
ODZ: 
, 
.
Gamit ang mga formula: 
, 
Isulat natin ang hindi pagkakapantay-pantay sa anyo: 
.
O, naniniwala 
pagkatapos ng mga simpleng pagbabagong nakukuha natin
,
,
.
Ang paglutas ng huling hindi pagkakapantay-pantay gamit ang paraan ng agwat, nakukuha namin:
Fig.4
, ayon sa pagkakabanggit 
. Pagkatapos mula sa Fig. 4 ang sumusunod 
, Saan 
.
Fig.5
Sagot: 
, 
.
1.4. Paraan ng pagitan
Pangkalahatang pamamaraan paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko gamit ang paraan ng agwat:
Sa pamamagitan ng paggamit mga formula ng trigonometriko factorize.
Hanapin ang mga discontinuity point at mga zero ng function at ilagay ang mga ito sa bilog.
Kumuha ng anumang puntoSA (ngunit hindi nahanap nang mas maaga) at alamin ang tanda ng produkto. Kung ang produkto ay positibo, pagkatapos ay maglagay ng isang punto sa labas ng bilog ng yunit sa ray na tumutugma sa anggulo. Kung hindi, ilagay ang punto sa loob ng bilog.
Kung ang isang punto ay nangyari ng kahit na bilang ng beses, tinatawag namin itong isang punto ng kahit multiplicity kung kakaibang numero beses - isang punto ng kakaibang multiplicity. Gumuhit ng mga arko tulad ng sumusunod: magsimula sa isang puntoSA , kung ang susunod na punto ay may kakaibang multiplicity, kung gayon ang arko ay nag-intersect sa bilog sa puntong ito, ngunit kung ang punto ay kahit multiplicity, hindi ito bumalandra.
Ang mga arko sa likod ng bilog ay mga positibong pagitan; sa loob ng bilog ay may mga negatibong espasyo.
Halimbawa 5. Lutasin ang hindi pagkakapantay-pantay
, 
.
Mga punto ng unang serye: 
.
Mga punto ng ikalawang serye: 
.
Ang bawat punto ay nangyayari sa isang kakaibang bilang ng mga beses, iyon ay, ang lahat ng mga punto ay may kakaibang multiplicity.
Alamin natin ang sign ng produkto sa 
: . Markahan natin ang lahat ng mga punto sa bilog ng yunit (Larawan 6):
kanin. 6
Sagot: 
, 
; 
, 
; 
, 
.
Halimbawa 6 . Lutasin ang hindi pagkakapantay-pantay.
Solusyon:
Hanapin natin ang mga zero ng expression .
Tumanggapaem :
,
;
, 
;
, 
;
, 
;
Sa mga halaga ng serye ng bilog ng unitX
1
kinakatawan ng mga tuldok 
. SeryeX
2
nagbibigay ng mga puntos 
. Isang seryeX
3
nakakakuha kami ng dalawang puntos 
. Sa wakas, ang seryeX
4
ay kumakatawan sa mga puntos 
. I-plot natin ang lahat ng mga puntong ito sa bilog ng unit, na nagpapahiwatig ng multiplicity nito sa mga panaklong sa tabi ng bawat isa sa kanila.
Hayaan ngayon ang numero 
magiging pantay. Gumawa tayo ng pagtatantya batay sa palatandaan:
Kaya, full stopA
dapat piliin sa sinag na bumubuo ng anggulo 
may sinagoh
sa labas ng bilog ng yunit. (Tandaan na ang auxiliary beamTUNGKOL SA
A
Hindi kinakailangan na ilarawan ito sa isang pagguhit. DotA
ay pinili nang humigit-kumulang.)
Ngayon mula sa puntoA
gumuhit ng isang kulot na tuloy-tuloy na linya nang sunud-sunod sa lahat ng minarkahang punto. At sa mga punto ang aming linya ay napupunta mula sa isang lugar patungo sa isa pa: kung ito ay nasa labas ng bilog ng yunit, pagkatapos ay papasok ito sa loob nito. Papalapit sa punto 
, ang linya ay babalik sa panloob na rehiyon, dahil ang multiplicity ng puntong ito ay pantay. Katulad sa punto 
(na may kahit multiplicity) ang linya ay kailangang paikutin panlabas na lugar. Kaya, gumuhit kami ng isang tiyak na larawan na ipinapakita sa Fig. 7. Nakakatulong ito upang i-highlight ang mga nais na lugar sa bilog ng yunit. Ang mga ito ay minarkahan ng "+" sign.
Fig.7
Panghuling sagot:
Tandaan. Kung ang isang kulot na linya, pagkatapos maglibot sa lahat ng mga puntong minarkahan sa bilog ng yunit, ay hindi maibabalik sa puntoA , nang hindi tumatawid sa bilog sa isang "ilegal" na lugar, nangangahulugan ito na ang isang error ay ginawa sa solusyon, ibig sabihin, isang kakaibang bilang ng mga ugat ang napalampas.
Sagot: .
§2. Isang hanay ng mga problema para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko
Sa proseso ng pagbuo ng kakayahan ng mga mag-aaral na malutas ang mga hindi pagkakapantay-pantay ng trigonometriko, 3 yugto ay maaari ding makilala.
1. paghahanda,
2. pagbuo ng kakayahan upang malutas ang mga simpleng trigonometriko hindi pagkakapantay-pantay;
3. pagpapakilala ng mga trigonometrikong hindi pagkakapantay-pantay ng iba pang mga uri.
Ang layunin ng yugto ng paghahanda ay kinakailangan na mabuo sa mga mag-aaral ang kakayahang gumamit ng isang trigonometriko na bilog o graph upang malutas ang mga hindi pagkakapantay-pantay, lalo na:
Kakayahang lutasin ang mga simpleng hindi pagkakapantay-pantay ng anyo ,
, ,
,
gamit ang mga katangian ng sine at cosine function;
Kakayahang bumuo ng dobleng hindi pagkakapantay-pantay para sa mga arko ng bilog na numero o para sa mga arko ng mga graph ng mga function;
Kakayahang magsagawa ng iba't ibang mga pagbabagong-anyo ng mga trigonometrikong expression.
Inirerekomenda na ipatupad ang yugtong ito sa proseso ng pag-systematize ng kaalaman ng mga mag-aaral tungkol sa mga katangian ng mga function ng trigonometriko. Ang pangunahing paraan ay maaaring mga gawain na inaalok sa mga mag-aaral at ginanap sa ilalim ng gabay ng isang guro o nang nakapag-iisa, pati na rin ang mga kasanayang binuo sa paglutas ng mga trigonometrikong equation.
Narito ang mga halimbawa ng mga naturang gawain:
1
. Markahan ang isang punto sa bilog ng yunit 
, Kung
.
2.
Saang quarter ng coordinate plane matatagpuan ang punto? , Kung 
katumbas ng: 
3.
Markahan ang mga puntos sa trigonometriko na bilog , Kung:
4. I-convert ang expression sa trigonometriko functionakoquarters.
A) 
,
b) 
,
V) 
5. Ibinigay ang Arc MR.M – gitnaako-th quarter,R – gitnaIIika-kuwarter. Limitahan ang halaga ng isang variablet para sa: (gumawa ng dobleng hindi pagkakapantay-pantay) a) arc MR; b) mga arko ng RM.
6. Isulat ang dobleng hindi pagkakapantay-pantay para sa mga napiling seksyon ng graph:
kanin. 1
7.
Lutasin ang hindi pagkakapantay-pantay 
, 
, 
, 
.
8. I-convert ang Expression .
Sa ikalawang yugto ng pag-aaral upang malutas ang mga hindi pagkakapantay-pantay ng trigonometriko, maaari kaming mag-alok ng mga sumusunod na rekomendasyon na may kaugnayan sa pamamaraan para sa pag-aayos ng mga aktibidad ng mag-aaral. Sa kasong ito, kinakailangang tumuon sa mga umiiral na kakayahan ng mga mag-aaral sa pagtatrabaho sa isang trigonometric na bilog o graph, na nabuo habang nilulutas ang pinakasimpleng mga equation ng trigonometriko.
Una, hikayatin ang pagiging posible ng pagkuha pangkalahatang pagpasok ang mga solusyon sa pinakasimpleng hindi pagkakapantay-pantay ng trigonometriko ay maaaring makamit sa pamamagitan ng pagbaling, halimbawa, sa isang hindi pagkakapantay-pantay ng anyo 
.
Gamit ang kaalaman at kasanayang nakuha sa yugto ng paghahanda, babawasan ng mga mag-aaral ang iminungkahing hindi pagkakapantay-pantay sa form 
, ngunit maaaring mahirapan na makahanap ng isang hanay ng mga solusyon sa nagresultang hindi pagkakapantay-pantay, dahil Imposibleng malutas ito gamit lamang ang mga katangian ng pag-andar ng sine. Ang kahirapan na ito ay maiiwasan sa pamamagitan ng pagpunta sa naaangkop na ilustrasyon (paglutas ng equation sa grapiko o paggamit ng unit circle).
Pangalawa, dapat maakit ng guro ang atensyon ng mga mag-aaral iba't-ibang paraan kumpletuhin ang gawain, magbigay ng angkop na halimbawa ng paglutas ng hindi pagkakapantay-pantay sa parehong graphical at paggamit ng trigonometriko na bilog.
Isaalang-alang natin ang mga sumusunod na solusyon sa hindi pagkakapantay-pantay .
1. Paglutas ng hindi pagkakapantay-pantay gamit ang unit circle.
Sa unang aralin sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko, mag-aalok kami sa mga mag-aaral ng isang detalyadong algorithm ng solusyon, na sa isang hakbang-hakbang na pagtatanghal ay sumasalamin sa lahat ng mga pangunahing kasanayan na kinakailangan upang malutas ang hindi pagkakapantay-pantay.
Hakbang 1.Gumuhit tayo ng unit circle at markahan ang isang punto sa ordinate axis 
at gumuhit ng isang tuwid na linya sa pamamagitan nito parallel sa x-axis. Ang linyang ito ay mag-intersect sa unit circle sa dalawang punto. Ang bawat isa sa mga puntong ito ay kumakatawan sa mga numero na ang sine ay katumbas ng .
Hakbang 2.Hinati ng tuwid na linyang ito ang bilog sa dalawang arko. Piliin natin ang isa na naglalarawan ng mga numero na may sinus na mas malaki kaysa . Naturally, ang arko na ito ay matatagpuan sa itaas ng iginuhit na tuwid na linya.
kanin. 2
Hakbang 3.Pumili ng isa sa mga dulo ng minarkahang arko. Isulat natin ang isa sa mga numero na kinakatawan ng puntong ito ng unit circle 
.
Hakbang 4.Upang mapili ang numero na tumutugma sa pangalawang dulo ng napiling arko, "lumakad" kami sa kahabaan ng arko na ito mula sa pinangalanang dulo hanggang sa isa pa. Kasabay nito, alalahanin na kapag kumikilos nang pakaliwa, ang mga numerong ating pagdadaanan ay tumataas (kapag lumipat sa tapat na direksyon, ang mga numero ay bababa). Isulat natin ang numero na inilalarawan sa bilog ng yunit sa pangalawang dulo ng minarkahang arko 
.
Kaya, nakikita natin ang hindi pagkakapantay-pantay matugunan ang mga numero kung saan totoo ang hindi pagkakapantay-pantay 
. Nalutas namin ang hindi pagkakapantay-pantay para sa mga numero na matatagpuan sa parehong panahon ng function ng sine. Samakatuwid, ang lahat ng mga solusyon sa hindi pagkakapantay-pantay ay maaaring isulat sa form 
Dapat hilingin sa mga mag-aaral na maingat na suriin ang pagguhit at alamin kung bakit ang lahat ng mga solusyon sa hindi pagkakapantay-pantay maaaring isulat sa anyo 
, 
.
kanin. 3
Kinakailangan na iguhit ang atensyon ng mga mag-aaral sa katotohanan na kapag nilulutas ang mga hindi pagkakapantay-pantay para sa pag-andar ng cosine, gumuhit kami ng isang tuwid na linya na kahanay sa ordinate axis.
Graphical na pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay.
Bumubuo kami ng mga graph 
At 
, Kung ganoon 
.
kanin. 4
Pagkatapos ay isulat namin ang equation 
at ang kanyang desisyon 
, 
, 
, natagpuan gamit ang mga formula 
, 
, 
.
(Pagbibigayn
mga halaga 0, 1, 2, nakita namin ang tatlong ugat ng pinagsama-samang equation). Mga halaga 
ay tatlong magkakasunod na abscissas ng mga intersection point ng mga graph At . Malinaw, palaging nasa pagitan 
hindi pagkakapantay-pantay hawak 
, at sa pagitan 
– hindi pagkakapantay-pantay 
. Interesado kami sa unang kaso, at pagkatapos ay pagdaragdag sa mga dulo ng agwat na ito ng isang numero na isang maramihang ng panahon ng sine, nakakakuha kami ng solusyon sa hindi pagkakapantay-pantay. bilang: 
, .
kanin. 5
Ibuod. Upang malutas ang hindi pagkakapantay-pantay , kailangan mong lumikha ng kaukulang equation at lutasin ito. Hanapin ang mga ugat mula sa resultang formula 
At 
, at isulat ang sagot sa hindi pagkakapantay-pantay sa form: , .
Pangatlo, ang katotohanan tungkol sa hanay ng mga ugat ng kaukulang hindi pagkakapantay-pantay ng trigonometriko Ito ay napakalinaw na nakumpirma kapag nilutas ito nang graphical.
kanin. 6
Kinakailangang ipakita sa mga mag-aaral na ang pagliko, na siyang solusyon sa hindi pagkakapantay-pantay, ay inuulit sa parehong pagitan, katumbas ng panahon ng trigonometriko function. Maaari mo ring isaalang-alang ang isang katulad na paglalarawan para sa graph ng function ng sine.
Pang-apat, ipinapayong magsagawa ng gawain sa pag-update ng mga diskarte ng mga mag-aaral para sa pag-convert ng kabuuan (pagkakaiba) ng mga function ng trigonometriko sa isang produkto, at upang maakit ang atensyon ng mga mag-aaral sa papel ng mga diskarteng ito sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko.
Ang ganitong gawain ay maaaring ayusin sa pamamagitan ng independiyenteng pagkumpleto ng mga mag-aaral sa mga gawain na iminungkahi ng guro, kung saan binibigyang-diin namin ang mga sumusunod:
Panglima, kailangang ilarawan ng mga mag-aaral ang solusyon sa bawat simpleng hindi pagkakapantay-pantay ng trigonometriko gamit ang isang graph o isang bilog na trigonometriko. Dapat mong tiyak na bigyang-pansin ang kapakinabangan nito, lalo na sa paggamit ng bilog, dahil kapag nilulutas ang mga hindi pagkakapantay-pantay ng trigonometriko, ang kaukulang paglalarawan ay nagsisilbing isang napaka-maginhawang paraan ng pagtatala ng hanay ng mga solusyon sa isang naibigay na hindi pagkakapantay-pantay.
Maipapayo na ipakilala sa mga mag-aaral ang mga pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko na hindi ang pinakasimpleng mga ayon sa sumusunod na pamamaraan: lumiko sa isang tiyak na hindi pagkakapantay-pantay ng trigonometric na lumiliko sa kaukulang trigonometric equation na magkasanib na paghahanap (guro - mga mag-aaral) para sa isang solusyon na independiyenteng paglipat ng nahanap na paraan sa iba pang hindi pagkakapantay-pantay ng parehong uri.
Upang ma-systematize ang kaalaman ng mga mag-aaral tungkol sa trigonometry, inirerekumenda namin ang espesyal na pagpili ng gayong mga hindi pagkakapantay-pantay, ang solusyon na nangangailangan ng iba't ibang mga pagbabagong maaaring ipatupad sa proseso ng paglutas nito, at ituon ang atensyon ng mga mag-aaral sa kanilang mga tampok.
Dahil sa mga produktibong hindi pagkakapantay-pantay maaari naming imungkahi, halimbawa, ang mga sumusunod:
Sa konklusyon, nagbibigay kami ng isang halimbawa ng isang hanay ng mga problema para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko.
1. Lutasin ang mga hindi pagkakapantay-pantay:
2. Lutasin ang mga hindi pagkakapantay-pantay: 3. Hanapin ang lahat ng solusyon sa mga hindi pagkakapantay-pantay: 4. Hanapin ang lahat ng solusyon sa mga hindi pagkakapantay-pantay:A) 
, nagbibigay-kasiyahan sa kondisyon 
;
b) 
, nagbibigay-kasiyahan sa kondisyon 
.
5. Hanapin ang lahat ng solusyon sa mga hindi pagkakapantay-pantay:
A) ;
b) ;
V) 
;
G) 
;
d) 
.
6. Lutasin ang mga hindi pagkakapantay-pantay:
A) ;
b) ;
V);
G) 
;
d);
e);
at) 
.
7. Lutasin ang mga hindi pagkakapantay-pantay:
A) 
;
b) ;
V);
G).
8. Lutasin ang mga hindi pagkakapantay-pantay:
A) ;
b) ;
V);
G) 
;
d) 
;
e);
at) 
;
h).
Maipapayo na mag-alok ng mga gawain 6 at 7 sa mga mag-aaral na nag-aaral ng matematika sa nakataas na antas, gawain 8 – para sa mga mag-aaral ng mga klase na may advanced na pag-aaral ng matematika.
§3. Mga espesyal na pamamaraan mga solusyon sa mga hindi pagkakapantay-pantay ng trigonometriko
Mga espesyal na pamamaraan para sa paglutas ng mga equation ng trigonometriko - iyon ay, ang mga pamamaraan na magagamit lamang upang malutas ang mga equation ng trigonometriko. Ang mga pamamaraan na ito ay batay sa paggamit ng mga katangian ng trigonometriko function, gayundin sa paggamit ng iba't ibang trigonometriko na mga formula at pagkakakilanlan.
3.1. Paraan ng sektor
Isaalang-alang natin ang pamamaraan ng sektor para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko. Paglutas ng mga hindi pagkakapantay-pantay ng form 
, SaanP
(
x
)
AtQ
(
x
)
– rational trigonometric functions (sines, cosines, tangents at cotangents ay kasama sa mga ito nang makatwiran), katulad ng paglutas ng mga rational inequalities. Ito ay maginhawa upang malutas ang mga nakapangangatwiran na hindi pagkakapantay-pantay gamit ang paraan ng mga pagitan sa linya ng numero. Ang analogue nito para sa paglutas ng mga makatwirang trigonometriko na hindi pagkakapantay-pantay ay ang paraan ng mga sektor sa trigonometric na bilog, para sasinx
Atcosx
(
) o trigonometric kalahating bilog para satgx
Atctgx
(
).
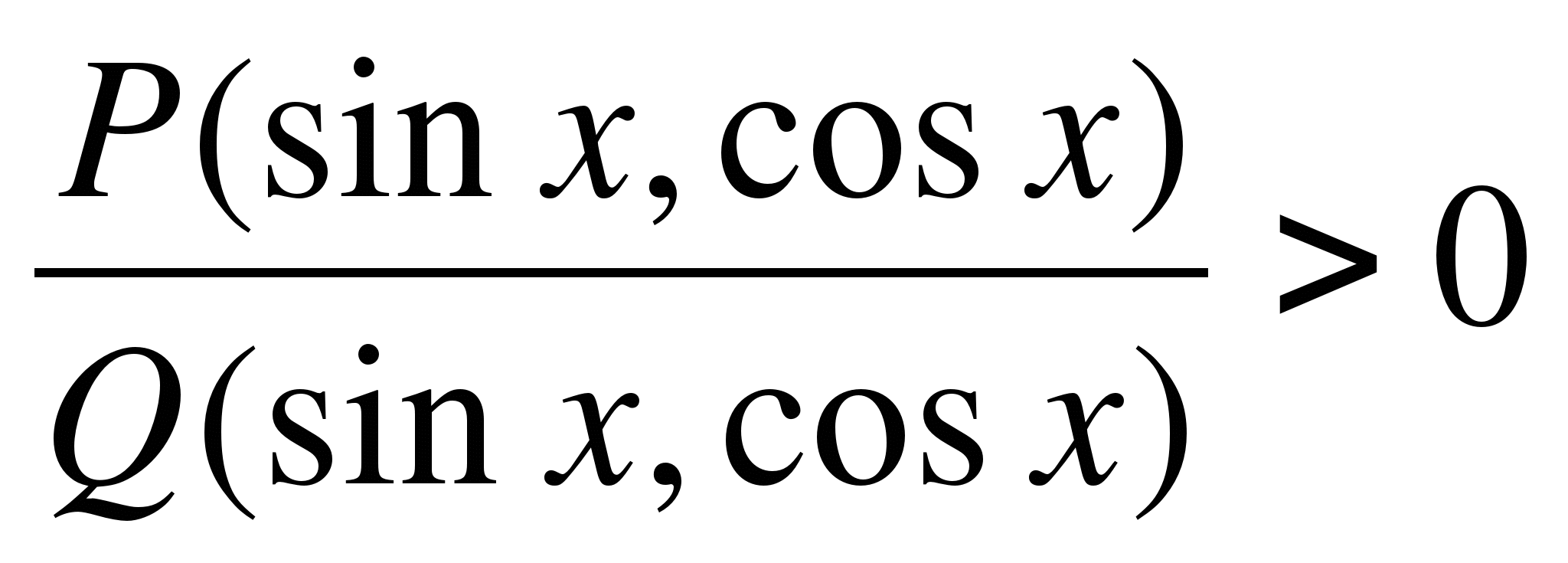
Sa paraan ng pagitan, ang bawat linear factor ng numerator at denominator ng form 
sa numerong axis ay tumutugma sa isang punto 
, at kapag dumadaan sa puntong ito pagbabago ng tanda. Sa pamamaraan ng sektor, ang bawat kadahilanan ng form 
, Saan 
- isa sa mga functionsinx
ocosx
At 
, sa isang trigonometric na bilog ay may katumbas na dalawang anggulo 
At 
, na naghahati sa bilog sa dalawang sektor. Kapag dumaan At function pagbabago ng tanda.
Ang mga sumusunod ay dapat tandaan:
a) Mga salik ng anyo 
At 
, Saan 
, panatilihin ang sign para sa lahat ng value 
. Ang ganitong mga salik ng numerator at denominator ay itinatapon sa pamamagitan ng pagbabago (kung 
) sa bawat ganitong pagtanggi, ang tanda ng hindi pagkakapantay-pantay ay binabaligtad.
b) Mga salik ng anyo 
At 
ay itinatapon din. Bukod dito, kung ito ay mga kadahilanan ng denominator, kung gayon ang mga hindi pagkakapantay-pantay ng anyo ay idinagdag sa katumbas na sistema ng mga hindi pagkakapantay-pantay. 
At 
. Kung ang mga ito ay mga kadahilanan ng numerator, kung gayon sa katumbas na sistema ng mga paghihigpit ay tumutugma sila sa mga hindi pagkakapantay-pantay. At sa kaso ng isang mahigpit na paunang hindi pagkakapantay-pantay, at pagkakapantay-pantay 
At 
sa kaso ng hindi mahigpit na paunang hindi pagkakapantay-pantay. Kapag itinapon ang multiplier 
o 
ang tanda ng hindi pagkakapantay-pantay ay nababaligtad.
Halimbawa 1.
Lutasin ang mga hindi pagkakapantay-pantay: a) 
, b) 
.
mayroon kaming function b) . Lutasin ang hindi pagkakapantay-pantay na mayroon tayo,
3.2. Paraan ng concentric na bilog
Ang pamamaraang ito ay isang analogue ng parallel number axes na paraan para sa paglutas ng mga sistema ng rational inequalities.
Isaalang-alang natin ang isang halimbawa ng isang sistema ng hindi pagkakapantay-pantay.
Halimbawa 5.
Lutasin ang isang sistema ng mga simpleng hindi pagkakapantay-pantay ng trigonometriko 
Una, hiwalay nating lutasin ang bawat hindi pagkakapantay-pantay (Larawan 5). Sa kanang sulok sa itaas ng figure, ipahiwatig namin kung aling argumento ang isinasaalang-alang ng trigonometriko na bilog.
Fig.5
Susunod, bumuo kami ng isang sistema ng mga concentric na bilog para sa argumentoX . Gumuhit kami ng isang bilog at lilim ito ayon sa solusyon ng unang hindi pagkakapantay-pantay, pagkatapos ay gumuhit kami ng isang bilog ng isang mas malaking radius at lilim ito ayon sa solusyon ng pangalawa, pagkatapos ay bumuo kami ng isang bilog para sa ikatlong hindi pagkakapantay-pantay at isang base na bilog. Gumuhit kami ng mga sinag mula sa gitna ng system sa pamamagitan ng mga dulo ng mga arko upang i-intersect nila ang lahat ng mga bilog. Bumubuo kami ng solusyon sa base na bilog (Larawan 6).
Fig.6
Sagot:
, 
.
Konklusyon
Nakumpleto ang lahat ng layunin ng pananaliksik sa kurso. Ang teoretikal na materyal ay systematized: ang mga pangunahing uri ng mga hindi pagkakapantay-pantay ng trigonometriko at ang mga pangunahing pamamaraan para sa paglutas ng mga ito ay ibinigay (graphical, algebraic, paraan ng mga agwat, sektor at ang paraan ng concentric na bilog). Ang isang halimbawa ng paglutas ng hindi pagkakapantay-pantay ay ibinigay para sa bawat pamamaraan. Ang teoretikal na bahagi ay sinundan ng praktikal na bahagi. Naglalaman ito ng isang hanay ng mga gawain para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko.
Ang coursework na ito ay maaaring gamitin ng mga mag-aaral upang pansariling gawain. Maaaring suriin ng mga mag-aaral ang antas ng karunungan sa paksang ito at magsanay sa pagkumpleto ng mga gawain na may iba't ibang kumplikado.
Napag-aralan ang kaugnay na literatura sa ang isyung ito Malinaw, maaari nating tapusin na ang kakayahan at kasanayan upang malutas ang mga hindi pagkakapantay-pantay ng trigonometriko sa kurso ng paaralan ng algebra at ang mga simula ng pagsusuri ay napakahalaga, ang pagbuo nito ay nangangailangan ng makabuluhang pagsisikap sa bahagi ng guro ng matematika.
kaya lang gawaing ito ay magiging kapaki-pakinabang para sa mga guro ng matematika, dahil ginagawang posible na epektibong ayusin ang pagsasanay ng mga mag-aaral sa paksang "Mga hindi pagkakapantay-pantay ng Trigonometric."
Ang pananaliksik ay maaaring ipagpatuloy sa pamamagitan ng pagpapalawak nito sa isang pangwakas na gawaing kwalipikado.
Listahan ng ginamit na panitikan
Bogomolov, N.V. Koleksyon ng mga problema sa matematika [Text] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 p.
Vygodsky, M.Ya. Handbook ng elementarya mathematics [Text] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 p.
Zhurbenko, L.N. Matematika sa mga halimbawa at problema [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.
Ivanov, O.A. Elementary mathematics para sa mga mag-aaral, mag-aaral at guro [Text] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.
Karp, A.P. Mga takdang-aralin sa algebra at ang simula ng pagsusuri para sa pag-aayos ng huling pag-uulit at sertipikasyon sa grade 11 [Text] / A.P. Carp. – M.: Edukasyon, 2005. – 79 p.
Kulanin, E.D. 3000 problema sa kompetisyon sa matematika [Text] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.
Leibson, K.L. Koleksyon mga praktikal na gawain sa matematika [Text] / K.L. Leibson. – M.: Bustard, 2010. – 182 p.
Siko, V.V. Mga problema sa mga parameter at ang kanilang solusyon. Trigonometry: mga equation, hindi pagkakapantay-pantay, mga sistema. Ika-10 baitang [Text] / V.V. siko. – M.: ARKTI, 2008. – 64 p.
Manova, A.N. Mathematics. Express tutor para sa paghahanda para sa Unified State Exam: mag-aaral. manwal [Text] / A.N. Manova. – Rostov-on-Don: Phoenix, 2012. – 541 p.
Mordkovich, A.G. Algebra at simula pagsusuri sa matematika. 10-11 baitang. Teksbuk para sa mga mag-aaral ng mga institusyong pangkalahatang edukasyon [Text] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 p.
Novikov, A.I. Trigonometric function, mga equation at hindi pagkakapantay-pantay [Text] / A.I. Novikov. – M.: FIZMATLIT, 2010. – 260 p.
Oganesyan, V.A. Mga paraan ng pagtuturo ng matematika sa sekondaryang paaralan: Pangkalahatang pamamaraan. Teksbuk manwal para sa mga mag-aaral ng pisika - banig. peke. ped. Inst. [Text] / V.A. Oganesyan. – M.: Edukasyon, 2006. – 368 p.
Olehnik, S.N. Mga equation at hindi pagkakapantay-pantay. Mga di-karaniwang pamamaraan mga desisyon [Text] / S.N. Olehnik. – M.: Factorial Publishing House, 1997. – 219 p.
Sevryukov, P.F. Trigonometric, exponential at logarithmic equation at hindi pagkakapantay-pantay [Text] / P.F. Sevryukov. – M.: Pampublikong edukasyon, 2008. – 352 p.
Sergeev, I.N. Pinag-isang Pagsusulit ng Estado: 1000 mga problema sa mga sagot at solusyon sa matematika. Lahat ng mga gawain ng pangkat C [Text] / I.N. Sergeev. – M.: Pagsusulit, 2012. – 301 p.
Sobolev, A.B. Elementary mathematics [Text] / A.B. Sobolev. – Ekaterinburg: State Educational Institution of Higher Professional Education USTU-UPI, 2005. – 81 p.
Fenko, L.M. Paraan ng mga agwat sa paglutas ng mga hindi pagkakapantay-pantay at pag-aaral ng mga function [Text] / L.M. Fenko. – M.: Bustard, 2005. – 124 p.
Friedman, L.M. Batayang teoretikal paraan ng pagtuturo ng matematika [Text] / L.M. Friedman. – M.: Book house “LIBROKOM”, 2009. – 248 p.
Annex 1
Graphic na interpretasyon ng mga solusyon sa mga simpleng hindi pagkakapantay-pantay
kanin. 1
kanin. 2
Fig.3
Fig.4
Fig.5
Fig.6
Fig.7
Fig.8
Appendix 2
Mga solusyon sa mga simpleng hindi pagkakapantay-pantay
Sa panahon ng praktikal na aralin, uulitin namin ang mga pangunahing uri ng mga gawain mula sa paksang "Trigonometry", bukod pa rito ay pag-aralan ang mga problema ng pagtaas ng pagiging kumplikado at isaalang-alang ang mga halimbawa ng paglutas ng iba't ibang mga hindi pagkakapantay-pantay ng trigonometriko at kanilang mga sistema.
Tutulungan ka ng araling ito na maghanda para sa isa sa mga uri ng gawain B5, B7, C1 at C3.
Magsimula tayo sa pamamagitan ng pagrepaso sa mga pangunahing uri ng mga gawain na tinakpan natin sa paksang "Trigonometry" at lutasin ang ilang hindi karaniwang mga problema.
Gawain Blg. 1. I-convert ang mga anggulo sa radian at digri: a) ; b) .
a) Gamitin natin ang formula para sa pag-convert ng mga degree sa radians
Palitan natin ang tinukoy na halaga dito.
b) Ilapat ang formula para sa pag-convert ng mga radian sa mga degree
Gawin natin ang pagpapalit 
.
Sagot. A); b) .
Gawain Blg. 2. Kalkulahin: a); b) .
a) Dahil ang anggulo ay lumampas sa talahanayan, babawasan natin ito sa pamamagitan ng pagbabawas ng sinus period. kasi Ang anggulo ay ipinahiwatig sa radians, pagkatapos ay isasaalang-alang namin ang panahon bilang .
b) B sa kasong ito pareho ang sitwasyon. Dahil ang anggulo ay ipinahiwatig sa mga degree, isasaalang-alang namin ang panahon ng tangent bilang .
Ang resultang anggulo, kahit na mas maliit kaysa sa tuldok, ay mas malaki, na nangangahulugang hindi na ito tumutukoy sa pangunahing, ngunit sa pinalawak na bahagi ng talahanayan. Upang hindi na muling sanayin ang iyong memorya sa pamamagitan ng pagsasaulo ng pinahabang talahanayan ng mga halaga ng trigofunction, ibawas natin muli ang tangent period:
Sinamantala namin ang kakaibang function ng tangent.
Sagot. a) 1; b) .
Gawain Blg. 3. Kalkulahin 
, Kung .
Bawasan natin ang buong expression sa tangents sa pamamagitan ng paghahati ng numerator at denominator ng fraction sa . Sa parehong oras, hindi namin maaaring matakot na, dahil sa kasong ito, hindi iiral ang tangent value.
Gawain Blg. 4. Pasimplehin ang expression.
Ang mga tinukoy na expression ay kino-convert gamit ang mga formula ng pagbabawas. Ang mga ito ay hindi karaniwang nakasulat gamit ang mga degree. Ang unang expression sa pangkalahatan ay kumakatawan sa isang numero. Pasimplehin natin ang lahat ng mga trigofunction nang paisa-isa:
kasi , pagkatapos ay nagbabago ang function sa isang cofunction, i.e. sa cotangent, at ang anggulo ay bumagsak sa ikalawang quarter, kung saan ang orihinal na tangent ay may negatibong tanda.
Para sa parehong mga kadahilanan tulad ng sa nakaraang expression, ang function ay nagbabago sa isang cofunction, i.e. sa cotangent, at ang anggulo ay bumagsak sa unang quarter, kung saan ang orihinal na tangent ay may positibong tanda.
Ipalit natin ang lahat sa isang pinasimpleng expression:
Problema #5. Pasimplehin ang expression.
Isulat natin ang tangent ng double angle gamit ang naaangkop na formula at pasimplehin ang expression:
Ang huling pagkakakilanlan ay isa sa mga pangkalahatang kapalit na formula para sa cosine.
Problema #6. Kalkulahin.
Ang pangunahing bagay ay hindi gumawa ng karaniwang pagkakamali ng hindi pagbibigay ng sagot na ang expression ay katumbas ng . Hindi mo maaaring gamitin ang pangunahing pag-aari ng arctangent hangga't mayroong isang kadahilanan sa anyo ng dalawa sa tabi nito. Upang mapupuksa ito, isusulat namin ang expression ayon sa formula para sa tangent ng isang dobleng anggulo, habang tinatrato ang , bilang isang ordinaryong argumento.
Ngayon ay maaari nating ilapat ang pangunahing katangian ng arctangent;
Problema Blg. 7. Lutasin ang equation.
Kapag nilulutas ang isang fractional equation na katumbas ng zero, palaging ipinapahiwatig na ang numerator ay katumbas ng zero, ngunit ang denominator ay hindi, dahil Hindi mo maaaring hatiin sa zero.
Ang unang equation ay isang espesyal na kaso ng pinakasimpleng equation na maaaring malutas gamit ang isang trigonometric na bilog. Tandaan ang solusyon na ito sa iyong sarili. Ang pangalawang hindi pagkakapantay-pantay ay nalulutas bilang ang pinakasimpleng equation gamit ang pangkalahatang pormula para sa mga ugat ng tangent, ngunit lamang sa sign na hindi pantay.
Tulad ng nakikita natin, ang isang pamilya ng mga ugat ay hindi kasama ang isa pang pamilya ng eksaktong parehong uri ng mga ugat na hindi nakakatugon sa equation. Yung. walang mga ugat.
Sagot. Walang mga ugat.
Problema Blg. 8. Lutasin ang equation.
Agad nating tandaan na maaari nating alisin ang karaniwang kadahilanan at gawin natin ito:
Ang equation ay nabawasan sa isa sa mga karaniwang anyo, kung saan ang produkto ng ilang mga kadahilanan ay katumbas ng zero. Alam na natin na sa kasong ito, alinman sa mga ito ay katumbas ng zero, o ang isa, o ang pangatlo. Isulat natin ito sa anyo ng isang hanay ng mga equation:
Ang unang dalawang equation ay mga espesyal na kaso ng pinakasimpleng mga equation nang maraming beses, kaya agad naming ipahiwatig ang kanilang mga solusyon. Binabawasan namin ang ikatlong equation sa isang function gamit ang double angle sine formula.
Lutasin natin ang huling equation nang hiwalay:
Ang equation na ito ay walang mga ugat, dahil ang halaga ng sine ay hindi maaaring lumampas 
.
Kaya, ang solusyon ay ang unang dalawang pamilya ng mga ugat lamang;
 |
Ito ay isang pamilya ng lahat ng kalahati, i.e.
Lumipat tayo sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko. Una, tingnan natin ang diskarte sa paglutas ng halimbawa nang hindi gumagamit ng mga formula pangkalahatang solusyon, ngunit gamit ang trigonometriko na bilog.
Problema Blg. 9. Lutasin ang hindi pagkakapantay-pantay.
Gumuhit tayo ng pantulong na linya sa trigonometriko na bilog na katumbas ng halaga ng sine na katumbas ng , at ipakita ang hanay ng mga anggulo na sumasagot sa hindi pagkakapantay-pantay.
 |
Napakahalaga na maunawaan nang eksakto kung paano ipahiwatig ang nagresultang pagitan ng mga anggulo, i.e. ano ang simula at kung ano ang wakas nito. Ang simula ng agwat ay ang anggulo na tumutugma sa punto na papasok tayo sa pinakadulo simula ng agwat kung kikilos tayo nang pakaliwa. Sa aming kaso, ito ang punto na nasa kaliwa, dahil paglipat ng pakaliwa at pagpasa sa tamang punto, kami, sa kabaligtaran, ay iniiwan ang kinakailangang hanay ng mga anggulo. Samakatuwid, ang tamang punto ay tumutugma sa dulo ng puwang.
Ngayon kailangan nating maunawaan ang mga anggulo ng simula at pagtatapos ng ating pagitan ng mga solusyon sa hindi pagkakapantay-pantay. Karaniwang pagkakamali- ito ay upang agad na ipahiwatig na ang tamang punto ay tumutugma sa anggulo, ang kaliwa at ibigay ang sagot. Hindi ito totoo! Mangyaring tandaan na ipinahiwatig lamang namin ang pagitan na naaayon sa itaas na bahagi ng bilog, bagaman interesado kami sa ibabang bahagi, sa madaling salita, pinaghalo namin ang simula at pagtatapos ng agwat ng solusyon na kailangan namin.
Para magsimula ang pagitan sa sulok ng kanang punto at magtatapos sa sulok ng kaliwang punto, kinakailangan na ang unang tinukoy na anggulo ay mas mababa sa dalawa. Upang gawin ito, kakailanganin nating sukatin ang anggulo ng tamang punto sa negatibong direksyon ng sanggunian, i.e. clockwise at ito ay magiging katumbas ng . Pagkatapos, simulang lumipat mula dito sa isang positibong direksyon sa clockwise, pupunta tayo sa tamang punto pagkatapos ng kaliwang punto at makuha ang halaga ng anggulo para dito. Ngayon ang simula ng pagitan ng mga anggulo ay mas mababa kaysa sa dulo, at maaari naming isulat ang pagitan ng mga solusyon nang hindi isinasaalang-alang ang panahon:
Isinasaalang-alang na ang mga naturang agwat ay mauulit ng walang katapusang bilang ng mga beses pagkatapos ng anumang integer na bilang ng mga pag-ikot, nakakakuha kami ng pangkalahatang solusyon na isinasaalang-alang ang sinus period:
Naglalagay kami ng mga panaklong dahil mahigpit ang hindi pagkakapantay-pantay, at pinipili namin ang mga punto sa bilog na tumutugma sa mga dulo ng pagitan.
Ihambing ang sagot na natanggap mo sa pormula para sa pangkalahatang solusyon na ibinigay namin sa panayam.
Sagot. 
.
Ang pamamaraang ito ay mabuti para sa pag-unawa kung saan nagmumula ang mga formula para sa mga pangkalahatang solusyon ng pinakasimpleng hindi pagkakapantay-pantay ng trigon. Bilang karagdagan, ito ay kapaki-pakinabang para sa mga masyadong tamad na matutunan ang lahat ng mga masalimuot na formula na ito. Gayunpaman, ang pamamaraan mismo ay hindi rin madali;
Upang malutas ang mga hindi pagkakapantay-pantay ng trigonometriko, maaari ka ring gumamit ng mga graph ng mga function kung saan itinayo ang isang pantulong na linya, katulad ng pamamaraang ipinakita gamit ang isang bilog na yunit. Kung interesado ka, subukang alamin ang diskarte na ito sa solusyon sa iyong sarili. Sa hinaharap ay gagamitin natin pangkalahatang mga formula para sa paglutas ng mga simpleng trigonometrikong hindi pagkakapantay-pantay.
Problema Blg. 10. Lutasin ang hindi pagkakapantay-pantay.
Gamitin natin ang formula para sa pangkalahatang solusyon, na isinasaalang-alang ang katotohanan na ang hindi pagkakapantay-pantay ay hindi mahigpit:
Sa aming kaso, nakukuha namin:
Sagot. 
Problema Blg. 11. Lutasin ang hindi pagkakapantay-pantay.
Gamitin natin ang pangkalahatang formula ng solusyon para sa kaukulang mahigpit na hindi pagkakapantay-pantay:
Sagot. 
.
Problema Blg. 12. Lutasin ang mga hindi pagkakapantay-pantay: a) ; b) .
Sa mga hindi pagkakapantay-pantay na ito, hindi na kailangang magmadali upang gumamit ng mga formula para sa mga pangkalahatang solusyon o ang trigonometriko na bilog, sapat na upang matandaan lamang ang hanay ng mga halaga ng sine at cosine.
a) Mula noon 
, kung gayon ang hindi pagkakapantay-pantay ay walang saysay. Samakatuwid, walang mga solusyon.
b) Dahil gayundin, ang sine ng anumang argumento ay laging nakakatugon sa hindi pagkakapantay-pantay na tinukoy sa kundisyon. Samakatuwid, ang lahat ng tunay na halaga ng argumento ay nakakatugon sa hindi pagkakapantay-pantay.
Sagot. a) walang mga solusyon; b) .
Suliranin 13. Lutasin ang hindi pagkakapantay-pantay 
.
1. Kung kumplikado ang argumento (iba sa X), pagkatapos ay palitan ito ng t.
2. Bumubuo kami sa isang coordinate plane toOy mga function graph y=gastos At y=a.
3. Nakikita natin ang ganyan dalawang magkatabing punto ng intersection ng mga graph, sa pagitan ng kung saan ay matatagpuan sa itaas ng tuwid na linya y=a. Natagpuan namin ang abscissas ng mga puntong ito.
4. Sumulat ng dobleng hindi pagkakapantay-pantay para sa argumento t, isinasaalang-alang ang panahon ng cosine ( t ay nasa pagitan ng mga natagpuang abscissas).
5. Gumawa ng reverse substitution (bumalik sa orihinal na argumento) at ipahayag ang halaga X mula sa dobleng hindi pagkakapantay-pantay, isinusulat namin ang sagot sa anyo ng isang numerical interval.
Halimbawa 1.
Susunod, ayon sa algorithm, tinutukoy namin ang mga halaga ng argumento t, kung saan matatagpuan ang sinusoid mas mataas tuwid. Isulat natin ang mga halagang ito bilang isang dobleng hindi pagkakapantay-pantay, na isinasaalang-alang ang periodicity ng cosine function, at pagkatapos ay bumalik sa orihinal na argumento X.
Halimbawa 2.
Pagpili ng hanay ng mga halaga t, kung saan ang sinusoid ay nasa itaas ng tuwid na linya.
Isinulat namin ang mga halaga sa anyo ng dobleng hindi pagkakapantay-pantay t, nagbibigay-kasiyahan sa kondisyon. Huwag kalimutan na ang pinakamaliit na panahon ng pag-andar y=gastos katumbas 2π. Pagbabalik sa variable X, unti-unting pinapasimple ang lahat ng bahagi ng double inequality.
Isinulat namin ang sagot sa anyo ng isang closed numerical interval, dahil ang hindi pagkakapantay-pantay ay hindi mahigpit.
Halimbawa 3.
Magiging interesado tayo sa hanay ng mga halaga t, kung saan ang mga punto ng sinusoid ay nasa itaas ng tuwid na linya.
Mga halaga t isulat ito sa anyo ng isang dobleng hindi pagkakapantay-pantay, muling isulat ang parehong mga halaga para sa 2x at ipahayag X. Isulat natin ang sagot sa anyong numerical interval.
At muli pormula gastos>a.
Kung gastos>a, (-1≤A≤1), pagkatapos - arccos a + 2πn< t < arccos a + 2πn, nєZ.
Mag-apply ng mga formula upang malutas ang mga hindi pagkakapantay-pantay ng trigonometriko at makakatipid ka ng oras sa pagsusulit sa pagsusulit.
At ngayon pormula
, na dapat mong gamitin sa UNT o Unified State Examination kapag nilulutas ang isang trigonometric inequality ng form gastos
Kung gastos , (-1≤A≤1), pagkatapos arccos a + 2πn< t < 2π — arccos a + 2πn, nєZ.
Ilapat ang formula na ito upang malutas ang mga hindi pagkakapantay-pantay na tinalakay sa artikulong ito, at mas mabilis mong makukuha ang sagot at nang walang anumang mga graph!
Isinasaalang-alang ang periodicity ng sine function, nagsusulat kami ng dobleng hindi pagkakapantay-pantay para sa mga halaga ng argumento t, nagbibigay-kasiyahan sa huling hindi pagkakapantay-pantay. Bumalik tayo sa orihinal na variable. Ibahin natin ang nagresultang dobleng hindi pagkakapantay-pantay at ipahayag ang variable X. Isulat natin ang sagot sa anyong pagitan.
Lutasin natin ang pangalawang hindi pagkakapantay-pantay:
Kapag nilulutas ang pangalawang hindi pagkakapantay-pantay, kinailangan naming baguhin ang kaliwang bahagi ng hindi pagkakapantay-pantay na ito gamit ang double argument sine formula upang makakuha ng hindi pagkakapantay-pantay ng form: sint≥a. Susunod na sinundan namin ang algorithm.
Nalutas namin ang ikatlong hindi pagkakapantay-pantay:
Mahal na mga nagtapos at mga aplikante! Tandaan na ang mga pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay ng trigonometriko, tulad ng paraang graphical na ibinigay sa itaas at, malamang na alam mo, ang paraan ng paglutas gamit ang isang yunit ng trigonometric na bilog (trigonometric na bilog) ay naaangkop lamang sa mga unang yugto ng pag-aaral ng seksyon ng trigonometrya. "Paglutas ng mga trigonometric equation at hindi pagkakapantay-pantay." Sa palagay ko ay maaalala mo na una mong nalutas ang pinakasimpleng mga equation ng trigonometriko gamit ang mga graph o isang bilog. Gayunpaman, ngayon ay hindi mo maiisip na lutasin ang mga trigonometrikong equation sa ganitong paraan. Paano mo sila malulutas? Tama iyon, ayon sa mga formula. Kaya dapat lutasin ang mga hindi pagkakapantay-pantay ng trigonometriko gamit ang mga formula, lalo na sa panahon ng pagsubok, kung kailan bawat minuto ay mahalaga. Kaya, lutasin ang tatlong hindi pagkakapantay-pantay ng araling ito gamit ang angkop na pormula.
Kung sint>a, kung saan -1≤ a≤1, pagkatapos arcsin a + 2πn< t < π — arcsin a + 2πn, nєZ.
Matuto ng mga formula!
At panghuli: alam mo ba na ang matematika ay mga kahulugan, tuntunin at FORMULA?!
Syempre ginagawa mo! At ang pinaka-mausisa, na pinag-aralan ang artikulong ito at napanood ang video, ay bumulalas: "Gaano katagal at mahirap! Mayroon bang formula na nagbibigay-daan sa iyong lutasin ang gayong mga hindi pagkakapantay-pantay nang walang anumang mga graph o bilog?" Oo, siyempre meron!
SA PAGSOLUSYON NG MGA HINDI PAGKAKATAYO NG FORM: kasalanan (-1≤A≤1) valid ang formula:
— π — arcsin a + 2πn< t < arcsin a + 2πn, nєZ.
Ilapat ito sa mga halimbawang tinalakay at mas mabilis mong makukuha ang sagot!
Konklusyon: ALAMIN ANG MGA FORMULA, MGA KAIBIGAN!
Pahina 1 ng 1 1